CHUNK 67 - the first 1300 words
TITLE Transformations
DESCRIPTION In this part of the book describe how shapes can be transformed.
OUTCOME Be able to use the transformation facilities in Processing to transform shapes previously introduced.
REFERENCE Greenberg 350--357
PROGRAM Develop a program that uses transformations of around 100-150 lines of code.

Processing has a number of functions which can be used to transform shapes. This chunk will describe how these can be used to draw any of the 2D primitive shapes introduced in chunk 66, but the same techniques will be used later on to transform more complex shapes such as those defined using OO classes as discussed in chunk 69. It's assumed that you have already read chunk 21 which discussed the basics of the coordinate system and how Processing uses this to display pixels on the screen.

The three functions that are needed for transforming shapes are:

      translate(), scale() and rotate() 

These don't merely take a shape and relocate or resize it, they alter the coordinate axes of the graphics context that will be used to display the shapes, so some understanding of how this works is necessary first of all.

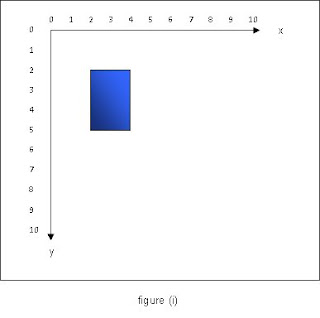
Figure (i) above shows a blue filled rectangle with width 2 and height 3 positioned with its top left hand corner at the point (2,2). Suppose xShift and yShift are the amounts the x and y axes respectively are to be translated by in the positive x and y directions. If the function:

       translate(xShift, yShift) 

is applied to the graphics context then the rectangle appears to be positioned on a different part of the screen. What is actually happening is that the coordinate system has changed and the origin has moved, so for example, if translate(2,3) is applied before drawing the rectangle, then the origin will move 2 units in the direction of the positive x axis and 3 units in the direction of the positive y axis, so that when the rectangle is drawn, its position will be that in figure (ii) below.

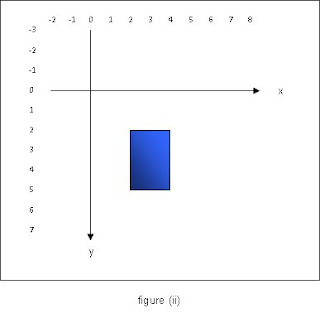
The rectangle will appear to be in a different place but the coordinates of its bounding box remain the same. It is of course quite possible to apply a translation which is large enough that shapes are no longer displayed on a visible part of the screen. This will become a problem once rotation is applied as will be explained later.

The effects of applying a scaling are similar. If xScaleFactor and yScaleFactor are the amounts by which the x and y axes are to be scaled, then applying the function:

       scale(xScaleFactor, yScaleFactor)

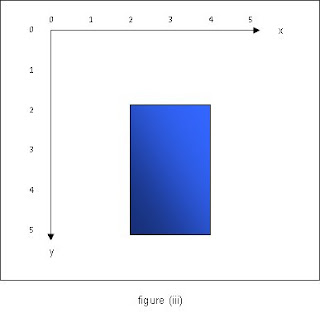
to the graphics context will have the effect of making shapes drawn on it appear bigger or smaller, depending on the size of the scale factor. Figure (iii) below shows what happens when scale(2,2) is applied before drawing the rectangle. It appears to be twice its original width and height and be positioned further away from the origin, but in fact the coordinates of its bounding box have remained unchanged.

Processing has a number of constants built in that are useful when working with rotations. PI was used in an earlier chunk but the remainder of these may be new to you:

Constant	Radians	(Degrees)
TWO_PI	2π	(360°)
PI	π	(180°)
HALF_PI	π/2	(90°)
QUARTER_PI	π/4	(45°)

Their values are in radians and they can be used as arguments, e.g.

       rotate(QUARTER_PI)

The rotate() function rotates the graphics context clockwise through the number of radians given by its argument. You might imagine that this function would be similar in concept to translate() and scale(), however there is an added complication here in that the centre of rotation of the graphics context is the origin. This means that, for example, if you rotated the axes about π/2, then the entire sketch would be outside the visible area. To understand why this is so, look at what appears to happen to the grey rectangle when rotate(HALF_PI) is applied. Figure (iv) below shows that the coordinate axes rotate clockwise through 90°, so that its new position is that of the blue rectangle.

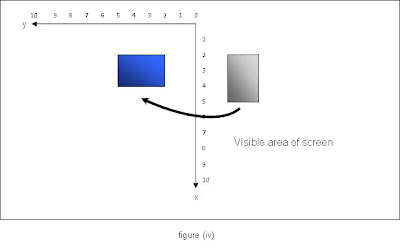
The visible portion of the screen is that to the right of the x axis. If the rectangle's location is as illustrated above, it won't be seen at all!

What is needed to rotate a shape around a different point, for example the centre of the screen, is first to translate the origin to the centre of the screen, then perform the rotation, and then translate the origin back again in the direction of the new axes by the same amounts as the original translation. Thus the following lines of code would rotate the graphics context through HALF_PI about the point (xShift, yShift):

      translate(xShift, yShift);
      rotate(HALF_PI);
      translate(-xShift, -yShift);

Rotation about the centre of the screen could be achieved by setting xShift to width/2 and yShift to height/2. Rotation about any other point can be achieved in the same way. Figure (v) below shows the effect of rotating the graphics context about the point (5,5) before drawing the same rectangle as before.

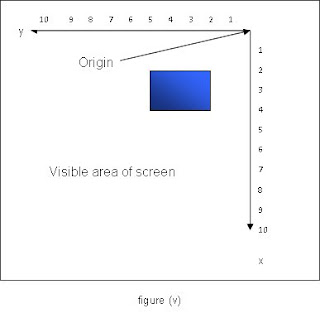
The coordinate axes are still rotated through 90°, but the origin has been translated first to the centre of the screen and then to the top right hand corner, so that the area bounded by the positive x and y axes is now visible.

The effects of the transformation functions are cumulative. That means that if you applied both scale() and translate() before drawing a shape then the coordinate axes would be scaled as well as the origin being translated. If you scaled them by 3 and then scaled them by 3 again, in both x and y directions, then the result would be to scale them by 3 * 3 = 9. A function resetMatrix() can be applied between transformations if this is not the intended effect. This changes the underlying affine transformation matrix back to its original settings. It's not necessary to consider the workings of this matrix in great detail here, but there's a reference [2] which explains the workings of the underlying Java AffineTransform class at the end of this chunk if you'd like to know more about how it works.

There is just one further consideration before we look at some examples of these functions in action. If the code to draw the shapes is placed in a draw() function, then on each iteration of the code within this, the affine transformation matrix will have been reset. This is equivalent to having performed resetMatrix() in each iteration of a loop. If you want to build up transformations cumulatively using draw(), then you will need a way to store the current transformation and restore it next time draw() is called. This is achieved using a matrix stack in Processing, as shown in figure (vi) below.

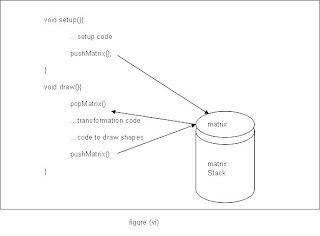
A call to popMatrix() at the start of the draw() function restores the affine transformation matrix by removing the top matrix from the stack and a call to pushMatrix() at the end of the function places the new affine transformation matrix at the top of the stack. A word of warning though; there has to be a matrix on the stack before you call popMatrix(), so setup() would also need a pushMatrix() call.